熱處理工藝是實現零部件微觀組織與性能調控的關鍵環節。熱處理本身是溫度、組織轉變與應力等交互作用的復雜過程［1 － 8］。因此在熱處理工藝實踐中，除微觀組織與性能的變外化，由于溫度場、結構等因素的影響，熱處理過程還會導致殘余應力與翹曲變形，對后續的機加和裝配過程帶來不利影響［6］。由于熱處理過程受到多個因素的交互影響，在實踐中很難通過物理模擬的方式進行研究，特別是熱處理發生在高溫階段，無法對組織、應力、變形等過程進行實時測量，室溫狀態的分析測試結果很難得到規律性成果。因此采用仿真技術對熱處理過程進行虛擬分析，對深入理解熱處理過程的組織、應力與溫度之間的相互影響規律，指導工藝設計具有重要意義。

鈦合金廣泛應用于航空、航天等對零件性能和精度要求高的領域，其熱處理工藝設計同樣面臨著組織性能調控、殘余應力與變形控制等難題。近二十年來，在鈦合金領域，研究者們在熱處理相變基礎理論、數值模型與軟件開發等方面開展了大量研究工作，熱處理工藝仿真在固溶時效、退火、熱校形等方面得到了深入應用，有助于深入理解鈦合金零部件工藝-組織-性能的關聯性、殘余應力與變形間產生制約機制，對熱處理工藝優化設計起到了很好地支撐作用。本文對鈦合金熱處理工藝仿真基礎理論與應用等方面展開綜述，并對未來的研究與應用方向提出展望，為鈦合金熱處理仿真在相關制造領域的應用提供參考。

1、熱處理仿真基礎理論與模型進展

鈦合金的熱處理過程包含溫度、組織轉變與應力三方面交互作用，最關鍵環節是針對相變和應力的數值模型。因此，目前大部分基礎理論與建模的進展主要集中在這兩方面。

鈦合金在熱處理過程中存在多種類型的相變，其中 β、α 相之間的轉變是最基本、最重要的一種，幾乎所有鈦合金在高溫冷卻或者時效過程中均會發生。鈦合金的 β 相為體心立方結構，而 α 相為密排立方 結 構，兩 相 之 間 存 在 嚴 格 的 Burgers 位 向 關系［9］。當冷卻速度較慢時，β-α 轉變受到溶質元素的擴散控制，兩相中的成分會有明顯不同。除此以外，當冷卻速度很大時，β 相轉換成 α 相的過程可能來不及進行，此時 β 相會發生馬氏體相變，轉變成與母相成分相同、晶體結構不同的過飽和固溶體，如六方馬氏體 α'和斜方馬氏體 α''，此時相變過程不發生元素擴散，主要發生晶格重構，轉變也沒有孕育期，相變動力學過程很快。從上面描述還可看出，鈦合金基體組織的相變機制與鋼鐵材料中的奧氏體分解過程比較類似，也存在擴散型和切邊型兩種類型的相變。同時許多試驗研究均表明，β-α 的擴散型相變也包含孕育期，相變動力學曲線也類似 S 型［10］。

因此，許多在鋼鐵材料中的熱處理微觀組織計算方法也可用于鈦合金相變過程的計算。最經典描述擴散型相變的方程是 Johnson-Mehl-Avrami-Kolmogorov( JMAK) 方程［11 － 13］，也被廣泛應用于鈦合金的相變動力學模擬。JMAK 方程是描述等溫過程的相變體積分 數 與 時 間 的 數 學 關 系，通 過 Schlie 疊 加 原則［14 － 16］，可將非等溫相變過程等價為多個微小等溫過程的疊加，從而實現任意溫度下的微觀組織預測，如圖 1 所示［4］。通過對經典 JMAK 方程的修正與發展，可進一步在模型中考慮初始母相晶粒度的影響［17］。鈦合金的 β 相轉變過程中，會形成多種形貌的 α 相組織。針對鈦合金的這種特性，JMAK 方程也被進一步發展，可用于預測等軸晶、針狀組織等不同形貌 α 相的體積分數及其動力學特性。Koistinen-Margurger( KM) 唯象模型及其變體形式被廣泛應用于鋼與鈦合金的馬氏體切變型相變［18 － 19］。KM 模型比較簡潔，相變分數與溫度之間的關系清晰明了，相關參數很容易確定，在軟件二次開發中很容易實現，但是 KM 模型不能準確描述馬氏體相變初始階段的動力學。

Lusk 等根據連續冷卻相變理論建立了針對擴散型相變與切變型相變的統一唯象模型［20］，這兩類相變的體積分數和溫度之間的關系可用公式( 1) 和( 2) 表示:

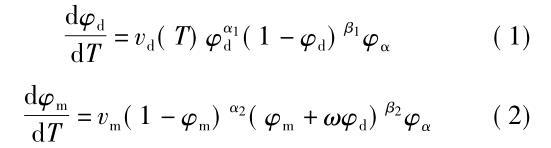
式中: φd 和 φm 表示擴散相變和切變相變組織的體積分數; φα 表示母相體積分數; vd 和 vm 為相變遷移率; α1、α2、β1、β2 和 ω 為相變動力學參數。相關參數通過擬合 CCT 連續冷卻相變曲線獲得。

熱處理過程中，與微觀組織相關的力學響應是另外一個重要的建模環節。由于熱處理過程的變形程度較小，為了準確描述其力學響應，其本構模型中必須要包含彈性和塑性，同時還要考慮卸載回彈的影響。為了與微觀組織建立關聯，目前比較合理的熱處理力學本構模型都是建立在單相的基礎上，針對每一種相變組織建立力學本構關系，然后整個材料的力學響應通過非線性混合法則來確定［1］。近年來，Bammann、Chiesa 和 Johnson 等從位錯理論出發，提出一種基于內變量的力學本構模型，這一模型最初主要用于塑性變形和切削加工等工藝領域。近年來，Bammann-Chiesa-Johnson 本構模型也被用于熱處理仿真，來描述每一種相的本構關系［21 － 24］。相比傳統的熱彈塑性模型，BCJ 模型不僅可以準確模擬回彈等因素對變形的影響，還可以實現和應變速率相關的力學響應預測，在較大的溫度區間和較大的變形速率范圍內，都有很高的模擬精度。根據 BCJ 模型，每一個相的屈服判據可以用如下公式描述:

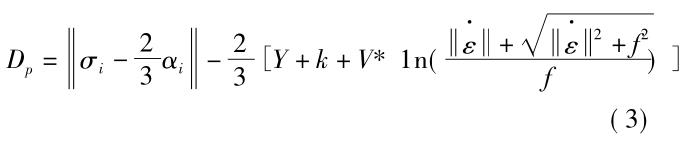
當 Dp≥0 時，對應相進入屈服狀態，否則仍處于彈性狀態。在公式( 3) 中，α 為張量內變量，k 為標量內變量，σ 為偏應力張量，Y 為率無關函數，V 和 f 為率相關函數。上述參數可以通過不同溫度下的單軸拉伸或壓縮應力-應變曲線擬合獲得。

在熱處理過程中，也必須考慮應力與相變的交互作用，其中一個重要的現象就是相變塑性。相變組織由于晶格參數的不同，往往會發生體積變化。

最典型的是在馬氏體相變過程中，會發生體積膨脹。這種膨脹會導致新相與母相之間發生相變誘導塑性現象，也就是在外加應力遠遠低于屈服應力狀態時發生的塑性變形。對整個變形影響較大，在實際過程中不可忽略。Greenwood 和 Johnson 建立了一個數學模型來描述這種相變過程中由于蠕變導致的塑性變形，在鋼鐵材料的熱處理仿真中得到了廣泛應用。相變塑性效應模型采用如下公式描述［25 － 26］:

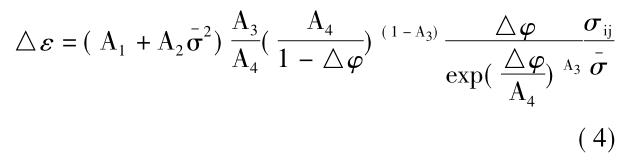
式中: △ε 為相變誘導塑性應變; σ 為等效應力; σij為偏應力張量; △φ 為相變組織體積分數; A2 為常數，可通過擬合伴隨相變的拉伸或壓縮應變-應變曲線獲得。這一模型在鋼鐵材料的相變中得到的廣泛應用，最近 Schuh 等人針對鈦合金的相變超塑性，發展了這一模型，將其擴展至非等溫的相變過程，并采用Ti-6Al-4V 合金的熱循環試驗對這一模型進行了驗證［27］。

2、熱處理仿真在鈦合金中的應用

達索公司的 Zhang 和 Chin 等以增材制造工藝為研究對象［28 － 29］，針對鈦合金增材制造冷卻與熱處理過程，構建出相變模擬框架，采用 KM 方程模擬快速冷卻過程的 β-α'馬氏體相變，JMAK 方程模擬鈦合金的 β-α 擴散型相變動力學，模型中考慮了 β 相的初始晶粒尺寸對相變動力學的影響，也可以進一步模擬 α' 相 的 板 條 束 寬 度［29］?；?于 這 一 框 架，在ABAQUS 中進行二次開發，成功預測了 TC4 鈦合金在增材制造過程中所得到的微觀組織( 圖 2) ，模擬結果與掃描電鏡的試驗結果吻合很好。

Semiatin 等構建出基于平均場理論的相變模型［30］，可模擬任意冷卻路徑下的初生 α 相晶粒尺寸和體積分數，也可擴展用于 TC4 和 Ti6242 合金中的雙態組織預測。將此模型和 DEFOＲM 有限元軟件結合，有限元模擬得到的零件局部位置冷卻路徑作為輸入條件，從而可模擬整個零件截面的微觀組織。

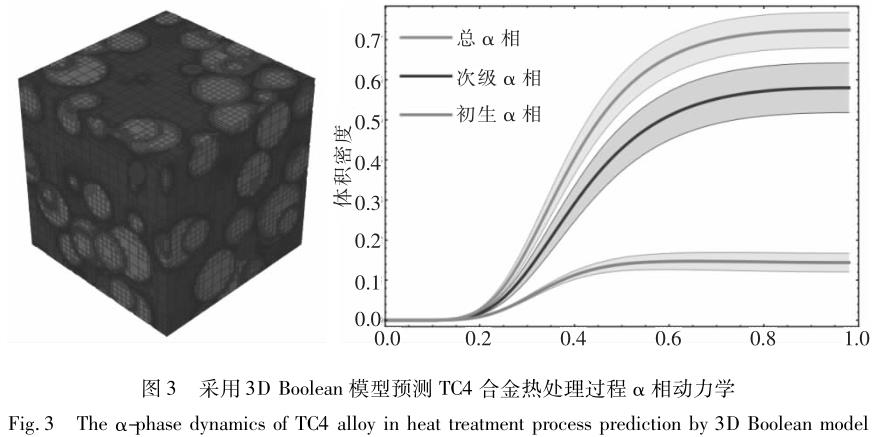
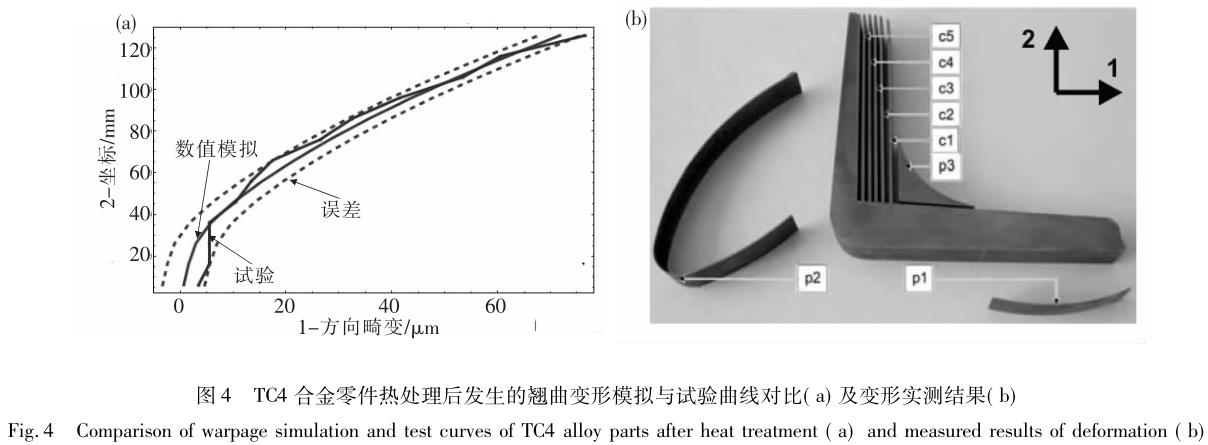
Ｒegner 等采用 Johnson-Mehl tessellation 和 Boolean 模型模擬 TC4 合金鍛造與熱處理過程初生 α 相的形成［31］，這一模型同樣基于平均場理論，可以與宏觀溫度場、變形場相互耦合計算求解，如圖 3 與圖 4 所示。Teixeira 等提出一個相變模型預測近 β 鈦合金在冷卻過程中的相變動力學［32 － 33］。采用 JMAK 模型計算晶內魏氏組織的相變動力學，采用形核-長大的平均場擴散理論模擬晶界 α 相和魏氏組織的動力學與形貌。該模型也可考慮因 β 相變形所帶來的 β相晶粒尺寸及亞晶對相變的影響。此模型在 Ti17 合金和 β-Cez 合金中應用，成功地預測了不同形態 α相的體積分數及其分布。Malinov 和 Sha 等通過 DSC試驗曲線推導出 JMAK 方程參數，用于模擬 β-α 相變后，α 晶粒的分數以及形貌［36］。

Schuh 等針對在外加應力條件下的鈦合金相變超塑性現象提出了一個數學模型，研究表明該模型可準確模擬加熱與冷卻循環過程中產生的應變增量。結合 JMAK 方程，就可以建立一個耦合模型，描述溫度-應力-相變之間的交互作用［27］。Malinov 等建立了神經網絡模型來模擬成分與工藝對鈦合金微觀組織及力學性能的影響［34 － 35］。由于神經網絡模型屬于黑箱算法，不涉及任何物理機制與建模，主要通過大量實驗數據建立工藝參數、成分與微觀組織、力學性能之間的關系。該模型最終決定的是微觀組織分數以及對力學性能的影響，無法對應力及翹曲變形進行仿真模擬。Krafft 等采用有限元軟件 Forge構建鈦合金熱處理過程的相變動力學計算模型。該模型不僅可實現 β 相和 α 相分數的預測，還可預測α 相的不同形貌及其占比。另外，此模型也常被用于 Ti17 和 Ti-6Al-4V 合金航空發動機壓氣機盤均勻化、鍛造、退火的加工全過程［37］。

Odenberger 等采用 Zener-Wert-Avrami 模型描述鈦合金的高溫應力松弛行為，如圖 5 所示［38］。王偉等基于經典 Norton 公式建立 Ti-6Al-4V 合金熱粘塑性本構模型［39，43］，在對初始殘余應力做假設和簡化基礎上，分析鈦合金薄板不同退火溫度對退火變形的影響規律，并結合試驗驗證模擬結果。劉向前等采用有限元法研究 TC4 薄壁圓筒件熱旋壓后的冷卻溫度場分布及冷卻后殘余應力與變形情況，在此基礎上，考慮旋壓過程的殘余應力，使用蠕變材料模型計算薄壁圓筒件去應力退火的變形情況［41］。由于 熱旋壓溫度以及退火溫度并未超過 β 相變點，因此在模擬過程中不用考慮基體相變的作用，主要考慮彈塑性以及蠕變塑性變形。王明偉等研究鈦合金真空熱處理及熱脹形過程數值模擬［42］，預測出加熱過程的滯后時間，并建立 BT20 鈦合金筒形件真空熱脹過程的熱力耦合有限元模型，得到可用于工業生產的工藝參數方案。陳濤等建立了 TC18 鈦合金退火態應力松弛行為的本構關系［40］，并用于長直桿件焊后退火熱處理過程的模擬，研究了退火加熱與冷卻過程的殘余應力與變形規律，結果為變形控制以及后續的熱校形工藝提供了指導依據。Alberg 等采用數值模擬的方法研究了航空發動機零部件焊接及焊后熱處理過程的畸變變形問題［44］。

3、總結與展望

近三十年來，鈦合金熱處理工藝仿真的基礎理論、數值模型與工程應用得到了長足發展，在微觀組織分布、殘余應力與翹曲變形預測等方面得到廣泛應用。目前，在熱處理工藝中，引入計算機模擬已成為加工制造業的發展趨勢，人們對材料熱處理過程采用計算機模擬重要性和意義的認識在不斷加深。

鈦合金熱處理過程的數值模擬雖已取得一定進展，但仍然面臨許多挑戰。例如，熱處理過程涉及到的外部因素復雜，除模型和算法的可靠性外，材料及介質參數的準確性也是非常關鍵的環節。這些參數包括熱物性參數( 導熱系數、熱容、熱膨脹系數、相變潛熱) 、力學性能參數( 彈性模量、泊松比、屈服強度、塑性模量) 、相變動力學參數、相變膨脹系數、相變塑性系數和淬火過程中的工件表面各處的換熱系數等［3］。以界面換熱系數為例，這一參數是決定工件溫度場分布的核心參數，與介質、工件以及實際的工藝實施方案密切相關。因此在實際熱處理仿真中，必須要結合現場實際條件進行測量和反求，才能讓模擬結果接近實際情況。此外，熱處理殘余應力和變形的高精度仿真仍然是一個難點，一方面殘余應力很難通過試驗進行準確驗證和校核，需要發展先進的殘余應力試驗技術對相關模型和算法進行驗證; 另一方面熱處理變形涉及到的溫度范圍寬，影響因素較多，對材料的本構模型與計算精度提出很高要求，需要進一步進行深入研究［1］。

近年來，基于介觀尺度的微觀組織演化計算方法也得到了很大的發展。以相場方法為代表的介觀計算方法可從機理上模擬鈦合金熱處理過程發生的相變［45 － 49］，不再局限于 JMAK 模型等平均場理論，可從單個晶粒的層次來模擬微觀組織演化，不僅可預測相變組織及其體積分數，還可預測組織形貌、溶質元素分布甚至新相變體取向規律。未來隨著計算機能力的增強以及算法的發展，有望將介觀尺度微觀組織演化計算方法與宏觀的溫度場以及應力/應變場進行耦合計算，從而使熱處理工藝仿真向多尺度方向發展，使材料設計與零部件制備有效結合起來。未來隨著基礎理論、模型和材料數據庫的不斷完善，熱處理技術終將擺脫憑經驗依賴，向精確預測、定量控制和設計制造一體化與智能化的方向飛躍。

參考文獻

［1］ Gur C H，Pan J S． Handbook of thermal process modeling of steels［M］． CＲS Press，2009．

［2］ 潘健生，張偉民，田東，等． 熱處理數學模型與計算機模擬［J］． 中國工程科學，2003( 5) : 47 － 54．

［3］Denis S，Sjostrom S，Simon A．Coupled temperature，stress，phase transformation calculation［J］． MetallurgicalTransactions A，1987( 18) : 1203 － 1212．

［4］SiMSiＲ C，Cemil Hakan GUＲ． A Mathematical Frame-work for Simulation of Thermal Processing of Materials ［J］． Application to Steel Quenching． Turkish Journal ofEngineering ＆ Enviromental Sicence，2008 ( 32) : 85 －100．

［5］劉莊，吳肇基，吳景之，等． 熱處理過程的數值模擬［M］． 北京: 科學出版社，1996．

［6］ Pan J S ，Li Y J，Gu J F，et al． Ｒesearch and application of computer on heat treatment process［J］． Journal of Shanghai Jiao Tong University ，2000E( 5) : 1 － 13．

［7］Inoue T ，Wang Z G． Coupling between stress，tempera-ture and metallic structures during processes involvingphase transformations［J］． Materials Science and Technolo-gy，1985( 10) : 845 － 850，

［8］Inoue T ，Funatani K，Totten G E． Process modeling for heat treatment:current status and future developments［J］． Journal of Shanghai Jiao Tong University，2000E( 5) : 14 － 25．

［9］趙永慶，陳永楠，張學敏，等． 鈦合金相變及熱處理［M］． 長沙: 中南大學出版社，2012．

［10］ Elmer J W，Palmer T A，Babu S S，et al． In situ observa-tions of lattice expansion and transformation rates of α andβ phases in Ti-6Al-4V［J］． Materials Science and Engi-neering: A 2005，391: 104 － 113．

［11］ Johnson W A，Mehl Ｒ F． Ｒeaction kinetics in processes of nucleation and growth transaction［J］． AIME，1939( 135) : 396 － 415．

［12］ Avrami M． Granulation，phase change，and microstruc-ture kinetics of phase change III［J］．The Journal of Chemical Physics，1941( 9) : 177 － 184．

［13］ Avrami M． Kinetics of phase change． I． General theory［J］． The Journal of Chemical Physics，1939( 7) : 1103 －1112．

［14］ Ｒéti T，Felde I． A non-linear extension of the additivity rule［J］． Computational Materials Science，1999 ( 15) :466 － 482．

［15］ Ye J S，Hsu T Y． Modification of the additivity hypothesis with experiment［J］． ISIJ International，2004( 44) : 777 －779．

［16］ Hsu T Y． Additivity hypothesis and effects of stress on phase transformations in steel［J］． Current Opinion in Sol-id State and Materials Science，2005( 9) : 256 － 268．

［17］ Hawbolt E，Chau B，Brimacombe J． Kinetics of austenite-pearlite transformation in eutectoid carbon steel［J］． Metal-lurgical Transactions A，1983( 14) : 1803 － 1815．

［18］ Lee S J，Lee Y K． Finite element simulation of quench distortion in a low-alloy steel incorporating transformation dinetics［J］． Acta Materialia，2008( 56) : 1482 － 1490．

［19］ Koistinen D P，Marburger Ｒ E． A general equation pre-scribing the extent of the austenite-martensite transforma-tion in pure iron-carbon alloys and plain carbon steels［J］．Acta Metallurgica，1959( 7) : 59 － 60．

［20］ Lusk M T，Lee Y K，Jou H J ，et al． An international state variable model for the low temperature tempering of low alloy steels［J］． Journal of Shanghai Jiao Tong Univer-sity，2000E( 5) : 178 － 184．

［21］ Bammann D，Hou H J． Development of a carburizing and quenching simulation Tool: A material model for steels un-dergoing phase transformations［A］． Proceeding of the sec-ond international conference on quenching and the control of distortion［C］． Cleveland，Ohio，1996．

［22］ Johnson G C，Bammann D J． Discussion of stress rates in finite deformation problems［J］． International Solids Struc-ture，1984( 20) : 725 － 736．

［23］ Bammann D J． An internal variable model of viscoplastici-ty［J］． International Journal of Engineering Science，1984( 22) : 1041 － 1051．

［24］ Li Z C，Ferguson B L． Effect of quenching rate on distor-tion and residual stresses during induction hardening of a full-float truck axle shaft［J］． Journal of Materials Engi-neering and Performance，2014( 23) : 4170 － 4180．

［25］ Greenwood G W，Johnson Ｒ H． The deformation of metals under small stresses during phase transformations［J］． Pro-ceedings of the Ｒoyal Society A: Mathematical，Physical and Engineering Sciences，1965，283: 403 － 422．

［26］ Leblond J B ，Devaux J． Mathematical modeling of trans-formation plasticity in steels I: Case of ideal-plastic phases［J］． International Journal of Plasticity，1989( 5) : 551 －572．

［27］ Schuh C，Dunand D C． Non-isothermal transformation-mismatch plasticity: modeling and experiments on Ti-6Al-4V［J］． Acta Materialia，2001( 49) : 199 － 210．

［28］ Zhang Q，Xie J，Gao Z，et al． A metallurgical phase transformation framework applied to SLM additive manu-facturing processes［J］． Materials ＆ Design，2019，166:107618．

［29］ Chin C． Additive manufacturing process simulation valida-tions and microstructure prediction［J］．

［30］ Semiatin S L，Knisley S L，Fagin P N，et al． Microstruc-ture evolution during alpha-beta heat treatment of Ti-6Al-4V［J］． Metall and Mat Trans A，2003，34: 2377 － 2386．

［31］ Ｒegener，Krempaszky B C，Stockinger E W M． Innova-tive forging and heat treatment simulation of titanium alloys ［A］． VPE Swiss Symposium，2013．

［32］ Teixeira D，Julien，Appolaire B，et al． Modeling of the phase transformations in near-β titanium alloys during the cooling after forging［J］． Computational Materials Science 2008，42: 266 － 280．

［33］ Julien Ｒ，Velay V．Characterization and modeling of forged Ti-6Al-4V titanium alloy with microstructural con-siderations during quenching process ［J］． International Journal of Mechanical Sciences，2018( 142 /143) : 456 －467．

［34］ Malinov S，Sha W． The neural network modeling of titani-um alloy phase transformation and mechanical properties ［J］． JOM，2005，57: 54 － 57．

［35］ Malinov S，Sha W． Modelling the correlation between pro-cessing parameters and properties in titanium alloys using artificial neural network［J］． Computational Materials Sci-ence，2001，21: 375 － 394．

［36］ Malinov S，Sha W． Modeling thermodynamics，kinetics，and phase transformation morphology while heat treating ti-tanium alloys［J］． JOM，2005，57: 42 － 45．

［37］ Krafft O，Settefrati A，Lasne P． The newest benefits of sim-ulation for heat treatment ＆ microstructure prediction［DB/OA］． http: / /www． transvalor． com/uploaded/ckeditor/files/Articles/FOＲGE/．

［38］ Odenberger E． Virtual process chain for superalloy ＆ tita-nium sheet metal aero engine structures validation and demonstrators［A］． Third International Workshop on Vali-dation of Computational Mechanics Models［C］．

［39］ 王偉，徐建軍，李華冠，等． 退火溫度對 Ti6A14V 薄板退火變形影響的有限元分析及實驗驗證［J］． 南京航空航天大學學報，2015，47( 5) : 737 － 744．

［40］ 陳濤． TC18 鈦合金熱變形行為與熱處理數值模擬［D］． 哈爾濱: 哈爾濱工業大學，2013．

［41］ 劉向前． TC4 鈦合金薄壁圓筒件熱成形后冷卻熱應力及變形模擬［D］． 哈爾濱: 哈爾濱工業大學，2005．

［42］ 王明偉． 高溫合金和鈦合金真空熱處理及熱脹形過程數值模擬［D］． 大連: 大連理工大學，2007．

［43］ 王偉，徐建軍，楊吟飛，等． Ti6Al4V 鈦合金薄板退火畸變數值模擬及試驗驗證［J］． 金屬熱處理，2016，41( 1) : 204 － 210．

［44］ Henrik Alberg． Simulation of welding and heat treatment modelling and validation ［D］． Lulea。，Sweden: Lulea。U-niversity of Technology，2005．

［45］ Chen Q，Ma N，Wang Y． Quantitative phase field model-ing of diffusion-controlled precipitate growth and dissolu-tion in Ti-Al-V［J］． Scripta Materialia，2004，50: 471 －476．

［46］ Steinbach I． Phase-field models in materials science［J］．Modelling and Simulation in Materials Science and Engi-neering，2009，17: 073001．

［47］ Qiu D，Shi Ｒ，Zhang D，et al． Variant selection by dislo-cations during α precipitation in α/β titanium alloys［J］．Acta Materialia，2015，88: 218 － 231．

［48］ Glavicic M G，Venkatesh V． Integrated computational ma-terials engineering of titanium: current capabilities being developed under the metals affordability initiative［J］．JOM，2014，66: 1310 － 1320．

［49］ Jou H J，Lusk M T． ． Comparison of Johnson-Meh1-Avra-mi-Kologoromov kinetics with a phase-field model for mi-crostructural evolution driven by substructure energy［J］．Physical Ｒeview B ，1997，55 ( 13) : 8114 － 8121．

相關鏈接